一笔画图形怎么判断
判断一个图形能否用一笔画完成(即欧拉路径问题),需要掌握以下核心方法:
图论基础概念 - 顶点(结点):图形中的交点或端点 - 边:连接两个顶点的线段 - 度数:与顶点相连的边的数量
关键判定标准 - 所有顶点度数为偶数:存在欧拉回路(起点=终点) - 恰好两个顶点度数为奇数:存在欧拉路径(起点≠终点) - 其他情况:不能一笔画
具体操作步骤 (1) 将图形转化为顶点和边的拓扑结构 (2) 统计每个顶点的度数 (3) 检查奇数度顶点的数量 (4) 根据判定标准得出结论
实际应用技巧 - 复杂图形可先简化去除已连通的偶数度顶点 - 观察图形中的"死胡同"(度数为1的顶点) - 桥梁结构(连接两个部分的唯一路径)需要特别注意
经典案例验证 - 五角星:所有顶点度数为2(可一笔画) - "日"字图形:4个顶点度数为3(不能一笔画) - 带对角线的矩形:2个顶点度数为3(可一笔画,需从奇数度顶点起笔)
常见误区提醒 - 图形是否闭合不影响判定(只影响起点终点是否重合) - 线条交叉但未形成新顶点不算作结点 - 孤立点不影响整体判定
掌握这些方法后,可通过以下练习巩固: ① 绘制七桥问题示意图进行验证 ② 分析汉字"田"、"中"的笔画可能性 ③ 设计可一笔画的自定义图案
一笔画图形的判断标准是什么?
判断一个图形是否能够一笔画成,主要依据以下两个核心标准:
连通性检查 图形必须是一个整体,所有线条都相互连接。如果图形中存在孤立的线条或部分,则无法一笔画成。检查方法:用手指或笔尖沿着线条移动,确保能够不抬起地到达所有部分。
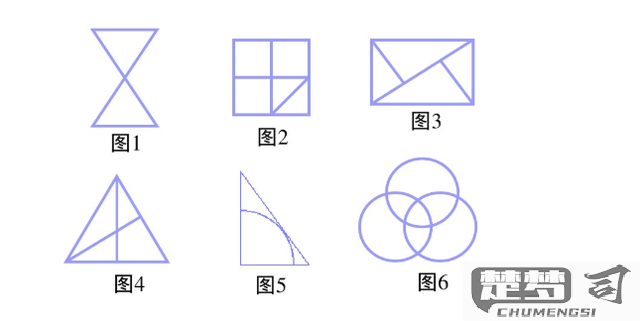
奇点数量分析 奇点指连接线条数量为奇数的交点(端点也算作奇点)。具体规则: - 当奇点数量为0时:图形可以一笔画成,且起点和终点重合(闭合图形) - 当奇点数量为2时:图形可以一笔画成,起点和终点分别为这两个奇点 - 当奇点数量为1或大于2时:图形不能一笔画成
实操步骤: 1. 用铅笔标记所有交点 2. 在每个交点处统计连接的线条数量(注意:经过该点的线条都算作连接) 3. 将连接数为奇数的交点圈出作为奇点 4. 根据奇点数量应用上述规则判断
示例验证: 以汉字"日"为例: - 检查连通性:所有横竖笔画均相连 - 分析奇点:四个角点各连接2条线(偶点),中间十字交点连接4条线(偶点) - 奇点数量为0,可以一笔画成且需回到起点
特殊情形处理: - 对于复杂图形,建议先分解为简单几何形状分析 - 包含曲线的情况同样适用,将曲线视为普通线条 - 自相交点(线条交叉但不连接)不计入连接数
如何快速判断一个图形是否可以一笔画成?
判断一个图形是否可以一笔画成(即存在欧拉路径),主要依据图论中的两个核心概念:顶点的度和图的连通性。具体操作步骤如下:
将图形转化为图论中的图结构 - 将图形中的每个交点或端点视为顶点 - 将图形中的每条线视为边
计算每个顶点的度数 - 度数是指连接到该顶点的边的数量 - 对于环形交点,每条进入和离开的边都计入度数
检查图的连通性 - 确保所有边都相互连接,没有孤立的子图 - 简单测试方法:任意两个顶点间都存在路径
应用欧拉路径判定规则 - 情况一:存在欧拉回路(起点终点相同) - 所有顶点的度数都是偶数 - 情况二:存在欧拉路径(起点终点不同) - 恰好有两个顶点的度数是奇数 - 其余所有顶点的度数都是偶数
快速判断技巧 - 数出图形中所有"奇数度顶点"的数量 - 数量为0或2时可以一笔画 - 数量为其他数值时不能一笔画
实例验证: - 五角星:5个顶点度数都是2(偶数)→ 可以一笔画(回路) - "日"字形:有2个顶点度数为3(奇数)→ 可以一笔画(路径) - "田"字形:有4个顶点度数为3(奇数)→ 不能一笔画
注意事项: - 自环边会使顶点度数增加2 - 重复边需要单独计算度数 - 图形必须能被笔不离纸地连续画出,不允许跳跃
一笔画图形的数学原理和技巧?
数学基础:欧拉路径与欧拉回路
- 欧拉路径:经过图中每一条边且每一条边只经过一次的路径
- 欧拉回路:起点和终点相同的欧拉路径
- 度数:与顶点相连的边的数量
判定条件
存在欧拉回路: - 所有顶点度数均为偶数 - 图是连通的
存在欧拉路径(非回路): - 恰好有两个顶点度数为奇数 - 图是连通的 - 这两个奇数度顶点分别为起点和终点
实用解题技巧
观察图形结构 - 先确认图形是否连通 - 计算每个交点的连线数量(度数)
确定起止点 - 当有2个奇数度顶点时,必须从其中一个出发 - 全偶数度时可从任意点出发
绘制策略 - 优先处理"死胡同"部分(仅一条连接的线段) - 避免过早封闭环形结构 - 对复杂图形可分区域处理
常见可一笔画图形 - 所有简单多边形 - 五角星及其变体 - 大多数字母形状(如O、I、L等)
练习方法
- 从简单图形开始(三角形、正方形)
- 逐步增加复杂度(添加内部线条)
- 尝试设计自己的可一笔画图形
- 记录绘制路径并分析优化方案
应用领域
- 电路板布线设计
- 物流路径优化
- 迷宫设计
- 儿童智力开发
典型练习图形示例:
•———•———•
| |
•———•———•
| |
•———•———•
(此矩形网格不可一笔画,因有超过2个奇数度顶点)
