年金现值系数怎么算
年金现值系数的计算需要明确几个关键参数:每期支付金额(A)、折现率(r)和期数(n)。计算公式为:
PVIFA = [1 - (1 + r)^-n] / r
计算步骤分解: 1. 确定折现率:将年利率转换为每期利率。例如年利率6%按年折现则r=0.06,按月折现则r=0.06/12 2. 计算(1+r)的值 3. 计算(1+r)的-n次方 4. 用1减去第三步的结果 5. 将第四步结果除以折现率r
示例计算(年支付1万元,5年期,年利率5%): 1. r=0.05 2. (1+0.05)=1.05 3. 1.05^-5≈0.7835 4. 1-0.7835=0.2165 5. 0.2165/0.05=4.329
因此年金现值系数为4.329,表示5年内每年1万元在5%折现率下的现值为43290元
注意事项: - 支付频率需与折现率周期匹配 - 期末年金默认计算公式,期初年金需乘以(1+r) - 精确计算建议使用金融计算器或Excel的PV函数
年金现值系数计算公式详解?
年金现值系数(Present Value of Annuity Factor,简称PVAF)是计算一系列等额现金流在当前时点价值的关键工具。其核心公式为:
[ PVAF = \frac{1 - (1 + r)^{-n}}{r} ]
参数解析: - r:每期折现率(如年利率5%则r=0.05) - n:现金流期数(如5年期的年金n=5)
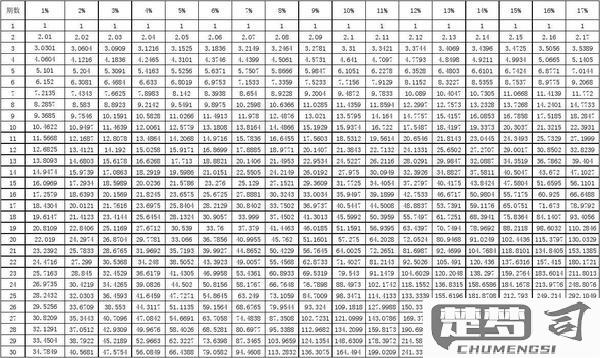
公式推导逻辑: 1. 将未来每期现金流A折现到当前时点: [ PV = A \times \left[ \frac{1}{(1+r)^1} + \frac{1}{(1+r)^2} + ... + \frac{1}{(1+r)^n} \right] ] 2. 提取公因式A后,括号内为等比数列求和,运用等比数列求和公式: [ S_n = \frac{1 - (1+r)^{-n}}{r} ]
实操案例: 假设每年末收到1000元,持续5年,年利率6%: [ PVAF = \frac{1 - (1+0.06)^{-5}}{0.06} = 4.2124 ] 现值 = 1000 × 4.2124 = 4212.4元
注意事项: 1. 区分普通年金(期末支付)与即付年金(期初支付): - 即付年金PVAF需乘以(1+r) 2. 利率与期数需匹配周期(月利率对应月份数) 3. 当r=0时,PVAF直接等于n(无折现效应)
Excel实现:
`excel
=PV(rate, nper, -1) / 注意参数顺序为利率、期数、固定支付额 /
`
典型应用场景: - 房贷月供计算 - 养老金规划 - 租赁付款评估
如何利用年金现值系数计算未来现金流现值?
计算未来现金流现值需要理解年金现值系数的核心作用。年金现值系数(PVIFA)是将一系列等额未来现金流折算为当前价值的乘数因子。
操作步骤:
确定关键参数 - 每期现金流金额(PMT) - 折现率(r):反映资金时间价值 - 期数(n):现金流的持续期限
获取年金现值系数 计算公式:
PVIFA = [1 - (1 + r)^-n] / r或查阅年金现值系数表计算现值
现值 = PMT × PVIFA(r,n)
实务案例:
假设每年收到10,000元,持续5年,年折现率5%:
1. 计算PVIFA:
[1 - (1+0.05)^-5]/0.05 = 4.3295
2. 计算现值:
10,000 × 4.3295 = 43,295元
注意事项: - 现金流间隔需固定(年/月/季) - 折现率应与现金流周期匹配 - 首期现金流发生在期末(普通年金) - 期初年金需调整系数:(1+r)×PVIFA
进阶应用: 对于非等额现金流,需分段计算: 1. 对等额部分使用年金系数 2. 对特殊金额单独折现 3. 加总各段现值
年金现值系数与折现率的关系是什么?
年金现值系数(PVIFA)与折现率之间存在反向变动关系。这种关系可通过数学表达式和实际应用两个层面理解:
数学本质
年金现值系数公式为:
[ PVIFA = \frac{1 - (1 + r)^{-n}}{r} ]
其中r为折现率,n为期数。当r增大时,分母(1+r)^n呈指数增长,导致分子[1 - (1+r)^-n]减小,最终使PVIFA值降低。折现率每上升1%,PVIFA的下降幅度呈非线性加速特征。经济逻辑
较高的折现率意味着:
- 资金时间价值增加,未来现金流的当前价值被更大幅度削减
- 投资者要求的回报率升高,相同年金流的吸引力下降
- 风险溢价上升时,补偿性折现会导致现值系数缩小敏感性特征
通过敏感性分析可发现:
- 长期年金(n>10年)对折现率变化更敏感
- 当折现率超过10%时,PVIFA的边际递减效应显著增强
- 在低利率环境(r<3%)下,折现率变化对PVIFA影响相对平缓实务应用要点
- 计算养老金负债时,若折现率从5%升至6%,30年期年金的现值系数会从15.372降至13.765(降幅10.45%)
- 资本预算决策中,建议建立折现率-PVIFA对照表,快速评估不同融资成本下的项目现值
- 使用Excel的PV函数验证时,注意参数设置:=PV(rate,nper,pmt,[fv],[type])特殊情形
当折现率为零时,PVIFA退化为简单加总(PVIFA=n),这是唯一不产生时间价值影响的特例。
