配对样本t检验的三线表是一种用于比较两个相关样本均值的统计方法，用于实验前后或配对数据的分析。此表格包含样本均值、标准差、样本量以及t值和p值等统计指标。关键的一点在于它能够有效地揭示在不同条件下的变化情况，从而帮助研究者判断实验处理对结果的影响是否显著。通过对配对样本t检验的分析，研究者能够得出关于样本之间差异的科学结论。
一、配对样本t检验的基本原理
配对样本t检验的基本原理是通过计算两个相关样本均值之间的差异来判断是否显著。对每对样本计算差值，求出这些差值的均值和标准差，最终利用t统计量进行检验。此方法适用于同一组受试者在不同条件下的测量，能够控制个体差异的影响，从而提供更为可靠的结论。
二、三线表的构建与解读
三线表的构建包括表头、数据区域和表底三部分，表头展示关键变量名称，如“组别”、“均值”、“标准差”等。数据区域则列出各组的统计数据，表底则t值和p值等重要检验结果。在解读时，研究者需要关注p值是否小于显著性水平（为0.05），以判断结果的显著性。均值差异的方向和大小也为结果的实际意义提供了依据。
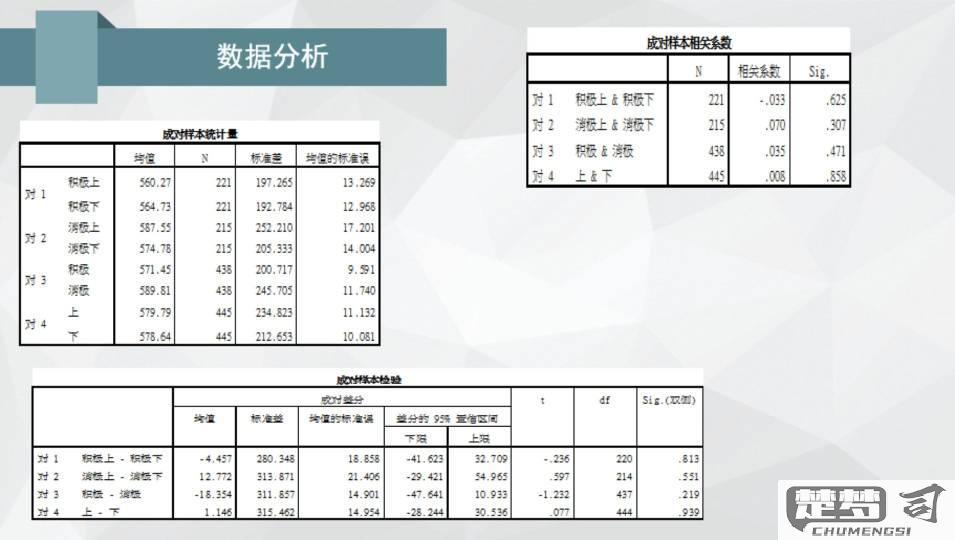
三、配对样本t检验的应用场景
配对样本t检验广泛应用于医学、心理学、教育等领域。在药物效果研究中，研究者可以在治疗前后分别测量患者指标，通过配对样本t检验判断药物是否有效。在教育研究中，教师可以通过对比学生在不同教学方法下的成绩变化，评估教学效果。此方法的灵活性和有效性使其成为研究中不可或缺的工具。
相关问答FAQs
问：什么情况下使用配对样本t检验？
答：当数据来自同一组受试者在不同条件下的测量时，治疗前后的体重变化、同一学生在不间的考试成绩等，适合使用配对样本t检验。
问：如何判断配对样本t检验的结果是否显著？
答：通过查看p值，p值小于设定的显著性水平（为0.05），则可以认为结果显著，说明两个相关样本均值之间存在统计学上的显著差异。
问：配对样本t检验对数据的要求是什么？
答：配对样本t检验要求数据符合正态分布，并且样本之间是配对的，即每一对数据都是相互关联的。
猜你感兴趣：
win10任务栏隐藏快捷键
上一篇
2025年01月21日
我设置了不看他的朋友圈
下一篇
2025年01月21日