求最小公倍数（LCM）的方法主要有三种：1. 分解质因数法；2. 采用最大公约数法；3. 列举法。这里我们重点讨论最大公约数法。该方法基于一个重要的数学定理：两个正整数的最小公倍数与它们的最大公约数的关系，可以用公式表示为：LCM(a, b) = (a × b) / GCD(a, b)。需要计算出两个数的最大公约数，利用这个关系式求得最小公倍数。这种方法不仅计算快捷，而且在处理较大的整数时尤为方便。
一、分解质因数法
分解质因数法是通过将每个数分解为质因数的形式来求最小公倍数。步骤为：将每个数分解为质因数，记录下每个质因数的最大指数。将所有质因数的最大指数相乘即为最小公倍数。这种方法在数较小时比较直观，但对于较大数值，分解过程会较为复杂。
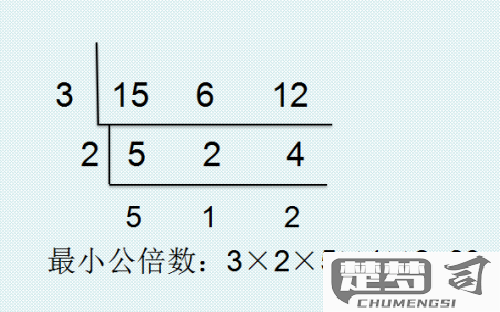
二、最大公约数法
如前所述，最大公约数法通过利用最大公约数来计算最小公倍数。这种方法不仅高效，而且可以通过算法（如欧几里得算法）实现最大公约数的快速计算，进而求得最小公倍数。该方法适用于任意正整数，并且在编程实现中更加灵活，适合处理大数据的问题。
三、列举法
列举法是最基础的求最小公倍数的方法，适合于小整数。步骤是列出每个数的倍数，直到找到它们的最小共同倍数。虽然这种方法简单易懂，但当涉及到较大的数字时，效率较低，且容易漏掉倍数，不太适合于复杂的计算。
FAQs
问：如何快速计算两个数的最大公约数？
答：可以使用欧几里得算法，它的基本思想是利用两个数的余数反复计算，直到余数为零时，另一个数即为最大公约数。
问：最小公倍数是否总是存在？
答：任何两个正整数的最小公倍数总是存在，并且是一个正整数。
问：最小公倍数和最大公约数有什么关系？
答：最小公倍数和最大公约数之间存在公式关系：LCM(a, b) = (a × b) / GCD(a, b)，这表明它们是相互关联的。
猜你感兴趣：
查询苹果手机系统的方法
上一篇
2024年12月27日
微信图片加载不出来一直转圈
下一篇
2024年12月27日