最大公因数是指两个或多个整数的共同因数中最大的那个,而最小公倍数则是指两个或多个整数的共同倍数中最小的那个。这两个概念在数论中具有重要的应用,尤其是在分数的简化、约分和求解相关问题时。最大公因数可以通过求解各个数的因数,找出其共同的最大值来获得,而最小公倍数则可以通过找出各个数的倍数,确定其最小的共同值。理解这两个概念不仅有助于解决数学问题,还能够提高逻辑思维能力。
一、最大公因数的计算方法
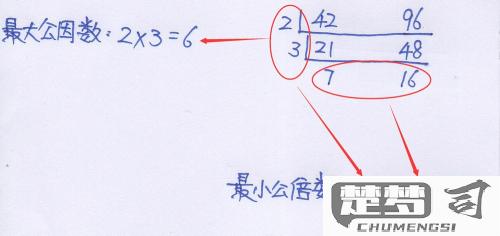
计算最大公因数的方法有多种,常见的包括因数法和辗转相除法。因数法是将两个数的所有因数列出,找出它们的共同因数,取最大的一个。而辗转相除法则是通过连续的整除操作来找到最大公因数,效率较高,尤其适合处理较大的数。
二、最小公倍数的计算方法
最小公倍数的计算方法有两种:倍数法和利用最大公因数来计算。倍数法是列出两个数的倍数,找到最小的共同倍数。而利用最大公因数的计算公式则是:最小公倍数 = (A × B) / 最大公因数,A和B是待求的两个整数。这种方法不仅简洁,而且计算效率高。
三、最大公因数与最小公倍数的关系
最大公因数和最小公倍数之间有着密切的关系。数学定理,两个数的乘积等于它们的最大公因数与最小公倍数的乘积。这一性质不仅为我们提供了计算的便利,也帮助我们理解这两个概念在数论中的重要性。
相关问答FAQs
问:最大公因数和最小公倍数有什么实际应用?
答:它们在许多实际问题中都有应用,在分数加减法中需要通分时,最小公倍数可以帮助找出共同的分母;而在简化分数时,最大公因数则用于约分。
问:如何快速找出两个数的最大公因数?
答:最有效的方法是使用辗转相除法,即将较大的数除以较小的数,用余数替代较大的数,再进行整除操作,直到余数为零,较小的数即为最大公因数。
问:最小公倍数是否总是比两个数中的较大者大?
答:不一定。两个数相同,那么它们的最小公倍数就是它们本身;一个数是另一个数的倍数,那么最小公倍数也会是较大的那个数。
