求最小公倍数的简便方法主要有以下步骤:1. 找出两个数的质因数分解;2. 记录每个质因数在两个数中出现的最大次数;3. 将这些质因数及其最大次数相乘,即可得到最小公倍数。这一方法的关键在于质因数分解,因为它能够清晰地显示出每个数的构成,便于我们识别和比较。
一、质因数分解的重要性
质因数分解是求最小公倍数的基础。通过将一个数分解为质数的乘积,我们可以直观地看到其所有的倍数。12的质因数分解为2² × 3¹,而18的质因数分解为2¹ × 3²。通过这些分解,我们能够有效地找出最小公倍数所需的质因数和其最高指数。
二、最大次数的选取
在进行质因数分解后,接下来的步骤是比较各质因数的次数。以12和18为例,质因数2在12中出现2次,在18中出现1次,所以我们在计算最小公倍数时选择2的最高次数2;质因数3在12中出现1次,在18中出现2次,选择3的最高次数2。这样,我们就能确保计算出的最小公倍数能够被这两个数整除。
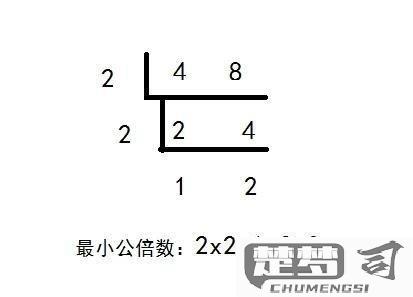
三、实例分析与应用
通过实例来说明这一方法的有效性。假设我们需要计算12和18的最小公倍数。进行质因数分解得到12=2² × 3¹,18=2¹ × 3²。记录质因数2和3的最大次数,得出2的最大次数为2,3的最大次数为2。将它们相乘:2² × 3² = 4 × 9 = 36。12和18的最小公倍数是36。这种方法不仅简单高效,而且适用于任何一对正整数。
相关问答FAQs
问:最小公倍数有什么实际应用?
答:最小公倍数在生活中有广泛的应用,在时间安排、工作计划、分配任务等方面,能够帮助我们找到合适的时间间隔,使得不同的任务能够协调进行。
问:求最小公倍数时,是否只有质因数分解一种方法?
答:除了质因数分解外,还有其他方法,如列举法和使用最大公约数法(LCM(a, b) = a × b / GCD(a, b))等。不过,质因数分解法因其系统性和直观性而被广泛使用。
问:是否可以用计算器求最小公倍数?
答:很多计算器和数学软件都提供了求最小公倍数的功能,用户只需输入要计算的数即可获得结果。这对于处理较大的数特别方便。
