找最大公因数的简单方法是使用辗转相除法(又称欧几里得算法)。这个方法的核心思想是,对两个数进行连续的除法运算,直到余数为零。步骤如下:将较大的数除以较小的数,得到一个商和一个余数,将较小的数替换为余数,再用之前的较小数除以新的较小数,重复这个过程,直到余数为零。一个非零余数就是这两个数的最大公因数。这个方法简单高效,适用于任意两个正整数。
一、辗转相除法的原理
辗转相除法的原理基于以下数学定理:两个整数的最大公因数等于较小的整数和它们的余数的最大公因数。通过不断替换和除法运算,可以逐步缩小问题的规模,最终找到最大公因数。这种方法不仅适用于两个数,也可以扩展到多个数,通过两两找出最大公因数。
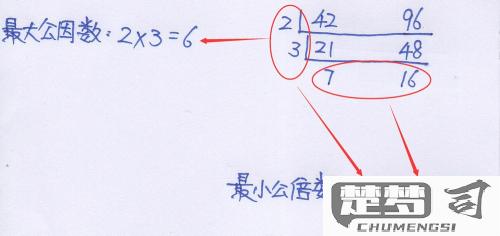
二、辗转相除法的步骤
步骤可以为:
1. 确定两个正整数A和B(A > B)。
2. 计算A ÷ B,得到余数R。
3. R = 0,则B即为最大公因数;R ≠ 0,则将A替换为B,将B替换为R,重复步骤2。
这个过程简单明了,能够快速找到结果。
三、辗转相除法的应用
辗转相除法不仅在数学中应用广泛,还可以用于解决实际问题,如简化分数、分析比例关系等。在编程中,这种算法也常被用来解决相关的数论问题,具有较高的计算效率和实用性。
相关问答FAQs
问:辗转相除法适用于哪些类型的数?
答:辗转相除法适用于任意两个正整数。对于负数或零,需先进行处理,确保输入为正整数。
问:如何将辗转相除法扩展到多个数?
答:可以将多个数两两进行比较,先找出前两个数的最大公因数,将这个结果与下一个数继续进行最大公因数的计算,直到所有数都处理完毕。
问:辗转相除法的时间复杂度如何?
答:辗转相除法的时间复杂度为O(log(min(A, B))),相对高效,尤其适合处理大数。
猜你感兴趣:
PPT演讲者模式设置在哪里
上一篇
excel去重保留唯一值
下一篇
