求两个数的最大公约数可以使用辗转相除法,这是一个基于整除原理的算法。其核心思想是:两个数的最大公约数等于较小数和较大数对其取余的结果的最大公约数。步骤为:设有两个数a和b(假设a > b),则最大公约数gcd(a, b)可以通过递归关系gcd(a, b) = gcd(b, a mod b)来求解,直到b为0,a即为所求的最大公约数。这个算法的时间复杂度是O(log(min(a, b))),在实际应用中效率很高。
一、辗转相除法的历史背景
辗转相除法源自古代数学,最早可追溯到《九章算术》。这一算法不仅简单易懂,而且适用于任意两个正整数,成为了计算最大公约数的重要工具。随着数学的发展,这一方法逐渐被普遍采用,并在现代计算机科学中得到了进一步的应用。
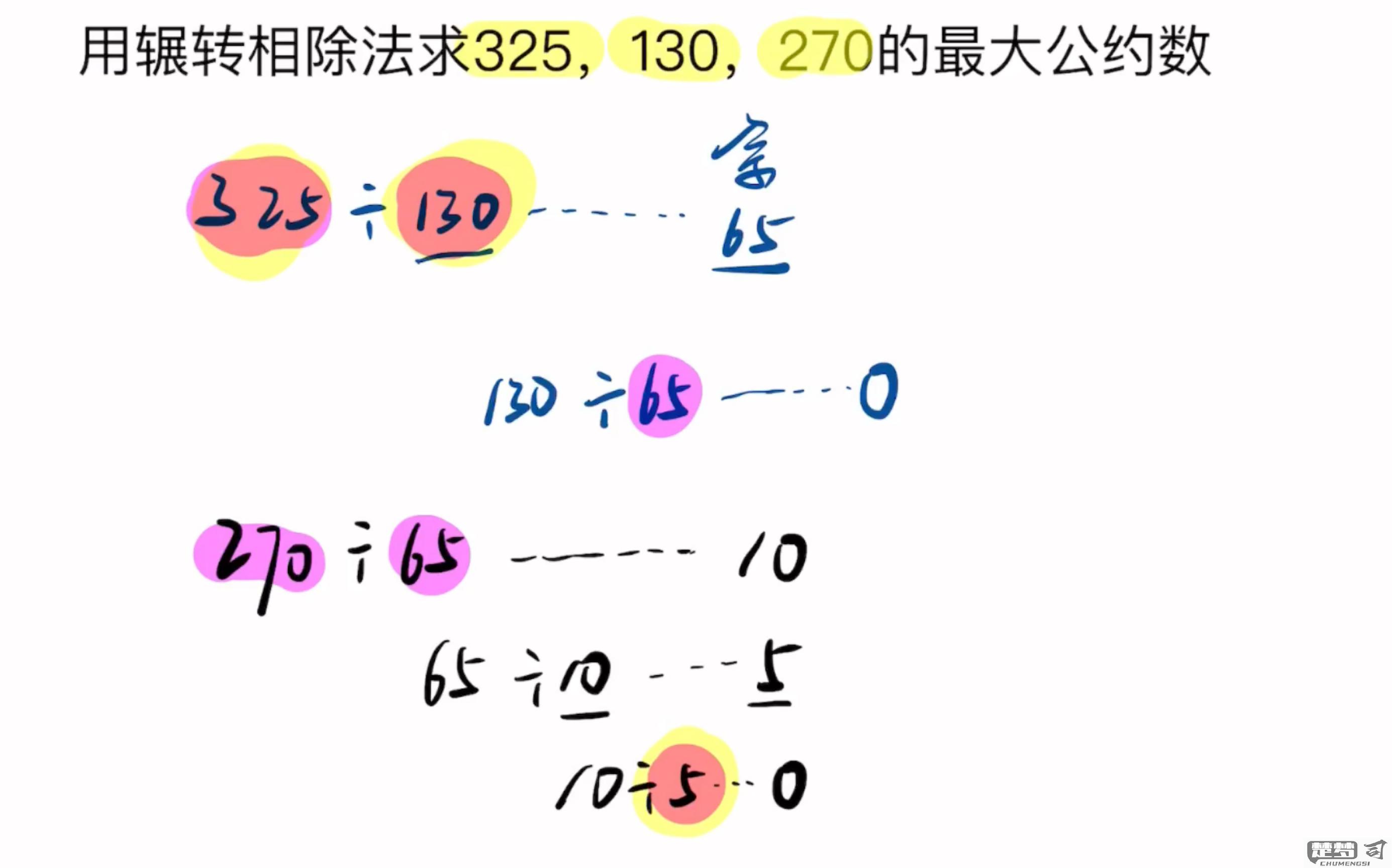
二、辗转相除法的实现步骤
实现辗转相除法的步骤如下:输入两个正整数a和b。判断b是否为0。b为0,则输出a作为最大公约数。不为0,则进行取余操作,计算a mod b,并将a赋值为b,将b赋值为a mod b。重复这一过程,直到b为0为止。最终,a即为所求的最大公约数。这种方法不仅直观,而且算法简单,易于编程实现。
三、辗转相除法的优势与局限性
辗转相除法的主要优势在于其高效性和通用性,特别是在处理大数时,性能表现优异。尽管其算法简单,但对于一些特殊情况,如输入数为0或负数时,需要额外的处理。辗转相除法虽然在计算复杂度上表现良好,但在实际应用中,对于极大的数,会面临内存和计算资源的限制。
相关问答FAQs
问:辗转相除法是如何处理负数的?
答:辗转相除法只适用于正整数。输入的数为负数,可以将其转化为对应的正数进行计算,因为最大公约数的定义仅涉及数的绝对值。
问:一个数为0,如何计算最大公约数?
答:定义,任何数和0的最大公约数为该数本身。输入的数为a和0,最大公约数gcd(a, 0) = |a|。
问:辗转相除法和更相减损法有什么区别?
答:更相减损法是另一种求最大公约数的方法,其通过不断减去较小的数来进行计算,而辗转相除法则使用取余操作。辗转相除法较为高效,尤其在数值较大时。
