一个数的负次方怎么算
计算一个数的负次方遵循数学中的指数法则。具体步骤如下:
理解负指数的含义
负指数表示倒数关系。对于任何非零数a和正整数n,公式为:
$$a^{-n} = \frac{1}{a^n}$$
例如:
$$2^{-3} = \frac{1}{2^3} = \frac{1}{8}$$分步计算示例
- 步骤1:先计算底数的正次方。
以5的-2次方为例,先计算5²=25。
- 步骤2:取结果的倒数。
$$5^{-2} = \frac{1}{25}$$特殊情况的处理
- 若底数为分数(如$\frac{2}{3}^{-4}$),先计算分数的正次方再取倒数:
$$\left(\frac{2}{3}\right)^{-4} = \left(\frac{3}{2}\right)^4 = \frac{81}{16}$$
- 零的负次方无意义(如0⁻³),因为分母不能为零。科学计算器的操作
输入顺序:
- 输入底数(如7)
- 按“^”或“xʸ”键
- 输入负指数(如-2)
- 按“=”显示结果(1/49)常见错误避免
- 勿将负号与减法混淆,$-3^2$表示先平方再取负(结果为-9),而$(-3)^2$才是9。
- 负指数的底数必须非零。
通过反复练习具体例子(如10⁻³=0.001,$\frac{1}{2}^{-5}$=32),可快速掌握负指数的计算逻辑。
一个数的负次方计算步骤详解?
计算一个数的负次方可以按照以下步骤进行:
理解负指数的含义 负指数表示该数的倒数。数学表达式为: a⁻ⁿ = 1 / aⁿ 其中a≠0,n为正整数
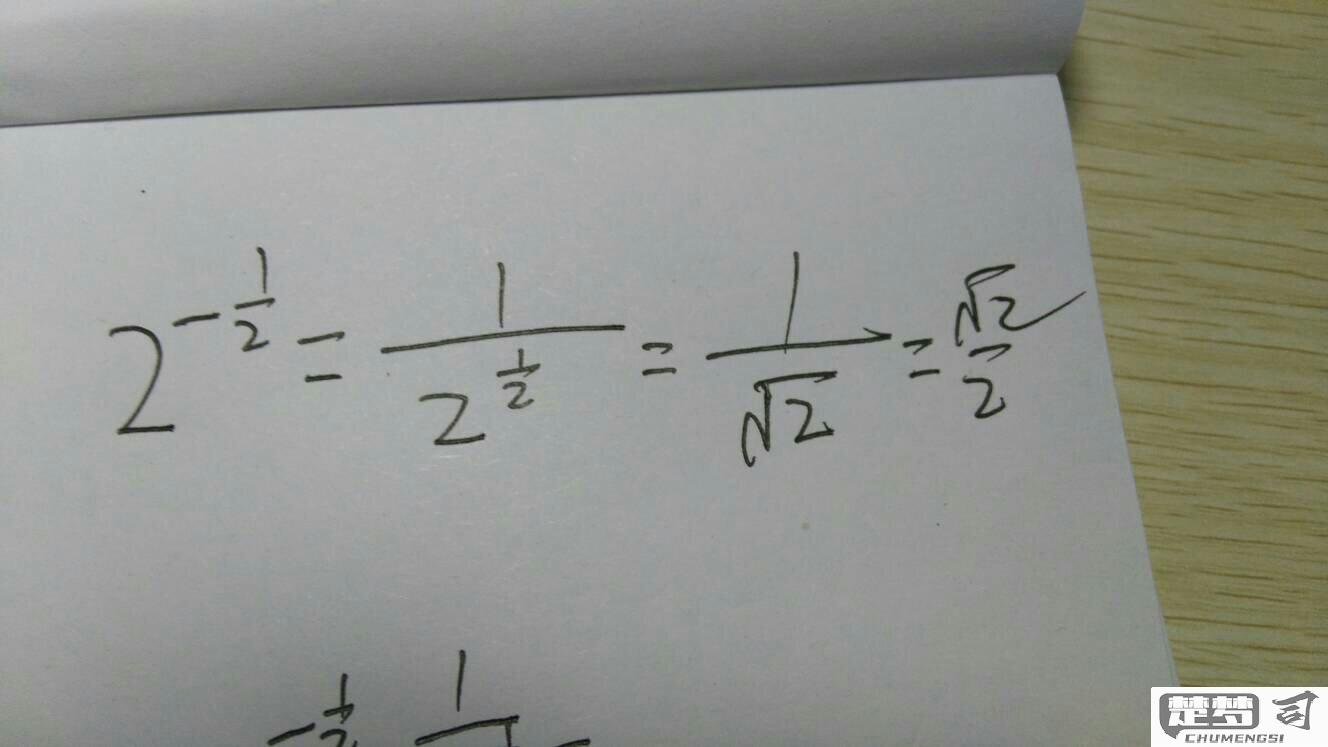
具体计算步骤 以计算2⁻³为例: - 将负指数转换为正指数:2⁻³ = 1 / 2³ - 计算分母的正指数:2³ = 2 × 2 × 2 = 8 - 取倒数:1 / 8 = 0.125
分数的情况 计算(3/4)⁻²: - 转换负指数:(3/4)⁻² = (4/3)² - 计算平方:(4/3)² = 16/9 ≈ 1.777...
十进制数的情况 计算0.5⁻²: - 转换负指数:0.5⁻² = (1/0.5)² = 2² - 计算结果:2² = 4
特殊情况 - 任何数的0次方都是1(a⁰=1) - 0的负次方无定义(0⁻ⁿ无意义)
负次方与分数次方的区别是什么?
负次方与分数次方是数学中两种不同的运算概念,它们在定义和运算规则上有本质区别:
负次方(Negative Exponents) - 定义:一个数的负次方等于该数倒数的正次方,即 ( a^{-n} = \frac{1}{a^n} ) - 核心性质:改变运算方向(从乘法变为除法) - 示例:( 2^{-3} = \frac{1}{2^3} = \frac{1}{8} ) - 运算优先级:与正次方相同,先计算次方再处理负号
分数次方(Fractional Exponents) - 定义:分数次方表示根式运算,( a^{m/n} = \sqrt[n]{a^m} ) - 分母为根指数,分子为被开方数的幂次 - 示例:( 8^{2/3} = \sqrt[3]{8^2} = \sqrt[3]{64} = 4 ) - 特殊形式:当m=1时,( a^{1/n} ) 就是n次方根
关键区别对比表: | 特征 | 负次方 | 分数次方 | |------------|---------------------|---------------------| | 数学本质 | 倒数运算 | 根式运算 | | 运算结果 | 改变量级大小 | 改变运算维度 | | 典型应用 | 科学计数法小数值表示 | 开方和无理数表示 | | 计算顺序 | 最后处理负号 | 先计算分数指数 |
计算技巧: - 混合运算时建议先处理分数次方再处理负号 - 遇到复杂表达式可转换为根式形式理解 - 负分数的次方需要特别注意运算顺序:( a^{-m/n} = \frac{1}{\sqrt[n]{a^m}} )
常见误区警示: - 错误认为负次方会使结果变小(实际上可能变大,如0.5^-1=2) - 混淆分数次方的分子分母位置 - 忽略负数底数的分数次方可能产生虚数的情况
如何快速计算一个数的负次方?
计算一个数的负次方可以通过以下步骤快速完成:
理解负次方的定义
负次方表示该数的倒数的正次方,即:
( a^{-n} = \frac{1}{a^n} )具体计算步骤
- 先计算底数的正次方结果
- 再取结果的倒数示例
- 计算 ( 2^{-3} ):
( 2^3 = 8 ),然后取倒数 ( \frac{1}{8} = 0.125 )
- 计算 ( 10^{-2} ):
( 10^2 = 100 ),倒数 ( \frac{1}{100} = 0.01 )特殊处理
- 底数为0时无意义(0的负次方未定义)
- 底数为分数时同样适用,如 ( \left(\frac{1}{2}\right)^{-3} = 2^3 = 8 )快速心算技巧
- 对于10的负次方,直接移动小数点:
( 10^{-n} ) = 小数点左移n位(如 ( 10^{-4} = 0.0001 ))
- 对于2的负次方,可记忆常见结果:
( 2^{-1}=0.5 ), ( 2^{-2}=0.25 ), ( 2^{-3}=0.125 ) 等计算器操作
输入顺序:
- 输入底数 → 按 ( x^y ) 键 → 输入负指数 → 按等号
或:
- 直接输入表达式如2^-3
