一元三次方程怎么解？详细步骤与实用方法全解析

一元三次方程怎么解

解一元三次方程的一般步骤如下：

1. 将方程化为标准形式： [ ax^3 + bx^2 + cx + d = 0 ] 其中 ( a \neq 0 )。

2. 除以首项系数 ( a )，得到简化形式： [ x^3 + px^2 + qx + r = 0 ] 其中 ( p = \frac{b}{a} )，( q = \frac{c}{a} )，( r = \frac{d}{a} )。

3. 通过变量替换 ( x = y - \frac{p}{3} ) 消去二次项，得到缺项形式： [ y^3 + my + n = 0 ] 其中： [ m = q - \frac{p^2}{3}, \quad n = r - \frac{pq}{3} + \frac{2p^3}{27} ]

4. 判别式分析： [ \Delta = \left( \frac{n}{2} \right)^2 + \left( \frac{m}{3} \right)^3 ] - 当 ( \Delta > 0 ) 时，方程有一个实根和两个共轭复根。 - 当 ( \Delta = 0 ) 时，方程有三个实根（可能有重根）。 - 当 ( \Delta < 0 ) 时，方程有三个不同的实根（三角解法）。

5. 求根公式： - 对于 ( \Delta \geq 0 ) 的情况： [ y = \sqrt[3]{ -\frac{n}{2} + \sqrt{\Delta} } + \sqrt[3]{ -\frac{n}{2} - \sqrt{\Delta} } ] - 对于 ( \Delta < 0 ) 的情况（三角解法）： [ y_k = 2\sqrt{ -\frac{m}{3} } \cos\left( \frac{1}{3} \arccos\left( \frac{3n}{2m} \sqrt{ -\frac{3}{m} } \right) - \frac{2k\pi}{3} \right) ] 其中 ( k = 0, 1, 2 )。

6. 最后将 ( y ) 的解代回 ( x = y - \frac{p}{3} ) 得到原方程的根。

实际计算时，建议使用计算器或数学软件辅助运算，特别是涉及复数运算或三角函数的部分。对于有理根的情况，可以尝试有理根定理（试根法）简化求解过程。

一元三次方程的标准解法步骤？

一元三次方程的标准解法步骤如下：

1. 将方程化为标准形式
   给定方程需整理为x³ + ax² + bx + c = 0的形式。若最高次项系数不为1，需两边同时除以该系数。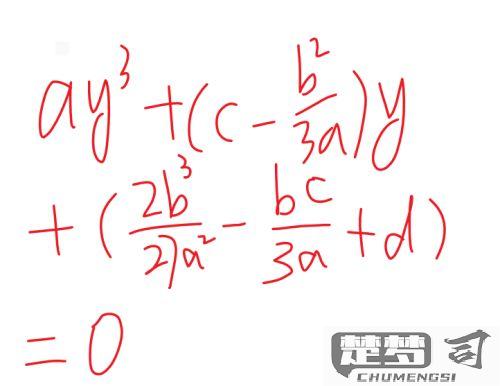

   

2. 进行变量代换消去二次项
   令x = y - a/3，代入后可消去y²项，得到简化形式y³ + py + q = 0。其中： p = b - a²/3
   q = c - ab/3 + 2a³/27

3. 判别式分析
   计算判别式Δ = (q/2)² + (p/3)³
   - Δ > 0：一个实根和两个共轭复根
   - Δ = 0：三个实根（至少两个相等）
   - Δ < 0：三个不同实根

4. 求解简化方程
   (1) 当Δ ≥ 0时：
   使用卡尔达诺公式：
   y = ∛(-q/2 + √Δ) + ∛(-q/2 - √Δ)

   (2) 当Δ < 0时（三角函数解法）：
   计算辅助角φ满足cosφ = -q/2√(-p³/27)
   三个实根为：
   y_k = 2√(-p/3)cos[(φ + 2kπ)/3], k=0,1,2

5. 回代求原方程的根
   将求得的y值通过x = y - a/3代回，得到最终解。

6. 验证结果
   将求得的根代入原方程验证正确性。

注意事项： - 计算过程中注意保持足够的计算精度 - 复数开立方需考虑三个不同立方根 - 实际计算推荐使用计算软件辅助

如何快速求解一元三次方程的实数根？

求解一元三次方程的实数根可采用以下步骤：

1. 方程标准化 将方程整理为x³ + ax² + bx + c = 0的标准形式

2. 判别式计算 计算判别式Δ = 18abc - 4a³c + a²b² - 4b³ - 27c² - Δ > 0：三个不同实数根 - Δ = 0：多重实数根 - Δ < 0：一个实数根和两个共轭复数根

3. 卡尔达诺公式求解 令p = b - a²/3 q = 2a³/27 - ab/3 + c 计算中间变量： u = ∛[-q/2 + √(q²/4 + p³/27)] v = ∛[-q/2 - √(q²/4 + p³/27)] 则实数根为： x1 = u + v - a/3

4. 特殊情况处理 当Δ=0时： - 三重根：x = -a/3 - 二重根和单根：x1 = (9c - ab)/(2b - 6a²) x2 = (4ab - 9c - a³)/(b - 3a²)

5. 数值解法（推荐） 对一般情况建议采用数值方法： - 牛顿迭代法：xₙ₊₁ = xₙ - f(xₙ)/f'(xₙ) - 二分法：在确定区间内逐步逼近

6. 实用建议 对于工程计算，可直接使用计算器或数学软件（如Matlab的roots函数）求解 手工计算时建议先尝试有理根定理测试简单有理根

一元三次方程解法的实际应用案例？

一元三次方程在实际中有广泛的应用价值，以下列举三个典型领域的应用案例：

1. 工程结构设计 在桥梁建设中，工程师需要计算拱桥的合理拱轴线方程。假设拱桥跨度为L，拱高为h，建立坐标系后拱轴线满足三次方程y=ax³+bx²+cx+d。通过测量关键点坐标代入方程，可解出参数确定最优拱形。

2. 经济学建模 某手机厂商分析定价与利润关系时，发现总利润P与单价x满足P=-0.5x³+120x²-5000x+20000。求导后得到三次方程-1.5x²+240x-5000=0，解此方程可找到利润最大化的最优定价点。

3. 物理运动分析 研究弹簧-质量系统非线性振动时，恢复力F与位移x的关系可能为F=kx³。当系统受迫振动时，运动方程化为mx''+kx³=F₀cosωt，通过变量代换可转化为三次方程求解特征频率。

具体解法建议： - 工程问题优先使用卡尔达诺公式 - 经济模型推荐数值解法（如牛顿迭代法） - 物理问题可尝试因式分解法

注意事项： 1. 实际应用中常出现Δ<0的情况，需使用三角函数解法 2. 建议结合MATLAB或Python的numpy.roots()函数验证手工解 3. 注意单位统一，特别是跨学科应用时