一元二次方程怎么算
解一元二次方程的标准形式为ax²+bx+c=0,主要掌握三种解法:
- 因式分解法(适用于整数解情况)
- 将方程整理为ax²+bx+c=0形式
- 寻找两个数m和n,满足: m×n=a×c m+n=b
- 将方程分解为(px+q)(rx+s)=0形式
- 令每个括号等于0得到解
示例:解x²+5x+6=0 寻找两个数满足乘积6且和为5,得到2和3 分解为(x+2)(x+3)=0 解得x=-2或x=-3
- 配方法(通用解法)
- 将方程整理为ax²+bx=-c
- 两边同除以a使x²系数为1
- 加上(b/2a)²完成配方
- 写成(x+d)²=e形式后开平方
示例:解2x²+8x-10=0 整理为x²+4x=5 配方:(x²+4x+4)=5+4 得到(x+2)²=9 解得x+2=±3 即x=1或x=-5
- 求根公式法(万能解法) 直接使用公式: x=[-b±√(b²-4ac)]/(2a)
计算步骤: - 计算判别式Δ=b²-4ac - Δ>0时有两个实数解 - Δ=0时有一个实数解 - Δ<0时无实数解
示例:解3x²-5x+1=0 计算Δ=(-5)²-4×3×1=13>0 代入公式: x=[5±√13]/6 得到两个解x=(5+√13)/6和x=(5-√13)/6
注意事项: - 优先检查能否因式分解 - 注意判别式的值判断解的情况 - 分数结果需要约分到最简 - 遇到复数解时可用i表示√(-1)
练习建议: 从整数解的简单方程开始练习因式分解 逐步过渡到含分数、无理数的复杂方程 最后掌握判别式与求根公式的完整应用
一元二次方程的标准形式是什么?
一元二次方程的标准形式为: [ ax^2 + bx + c = 0 ] 其中: - ( a ) 是二次项系数,且 ( a \neq 0 ) - ( b ) 是一次项系数 - ( c ) 是常数项
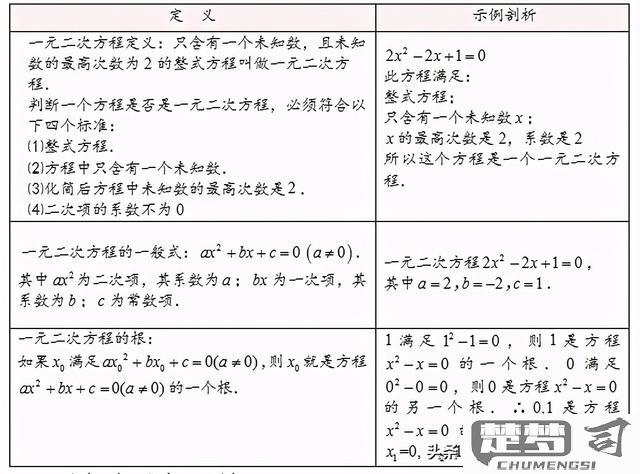
示例说明: 1. ( 2x^2 - 5x + 3 = 0 ) 是标准形式,对应 ( a=2 ), ( b=-5 ), ( c=3 ) 2. ( x^2 = 4 ) 需改写为 ( x^2 - 4 = 0 ) 才符合标准形式 3. ( 3x + 7 = 0 ) 不是二次方程,因为缺少 ( x^2 ) 项
判断标准形式的三个要点: 1. 方程必须整理为右边等于零的形式 2. 左边按 ( x ) 的降幂排列 3. 最高次项 ( x^2 ) 的系数不能为零
如何求解一元二次方程的根?
一元二次方程的标准形式为ax² + bx + c = 0(a≠0)。求解根的主要方法有三种:
因式分解法 适用于方程能分解为两个一次因式相乘的情况 步骤: - 将方程整理为(x + m)(x + n) = 0的形式 - 令每个因式等于0,得到x = -m和x = -n两个解
配方法 通用解法,适用于所有一元二次方程 步骤: - 将常数项移到等式右边:ax² + bx = -c - 两边同除以a:x² + (b/a)x = -c/a - 配方:x² + (b/a)x + (b/2a)² = (b/2a)² - c/a - 左边写成完全平方式:(x + b/2a)² = (b²-4ac)/4a² - 开平方求解
求根公式法 最直接的通用解法,公式为: x = [-b ± √(b²-4ac)] / (2a)
判别式Δ = b²-4ac决定根的性质: - Δ > 0:两个不等实根 - Δ = 0:两个相等实根 - Δ < 0:一对共轭复根
计算示例: 解方程2x² + 5x - 3 = 0 a=2, b=5, c=-3 Δ = 5² - 4×2×(-3) = 25 + 24 = 49 > 0 x = [-5 ± √49]/4 = (-5 ± 7)/4 得x₁ = (-5+7)/4 = 0.5,x₂ = (-5-7)/4 = -3
一元二次方程在实际生活中的应用案例?
一元二次方程在实际生活中的应用非常广泛,以下是几个典型场景及详细解析:
建筑设计与施工 - 拱形结构计算:拱桥或穹顶设计中,抛物线形状(y=ax²+bx+c)需通过解方程确定关键参数。例如计算拱桥最高点离水面高度时,已知两点坐标和水面方程即可建立方程组。 - 材料优化:确定矩形截面梁的抗弯性能时,在固定周长下求最大面积问题可转化为二次方程求极值。
运动轨迹预测 - 投掷运动:篮球投篮轨迹符合h=-5t²+vt+h₀(h为高度,t为时间,v为初速)。若需计算3秒后是否到达3米高度,直接代入求解。 - 导弹拦截:防御系统通过解来袭导弹与拦截弹的轨迹方程组计算碰撞点。
经济决策分析 - 盈亏平衡点:已知总成本C=2x²+5x+1000和总收入R=50x,令C=R解得x值即为保本销量。 - 最优定价:利润P=-2p²+300p-5000(p为单价),通过顶点公式p=-b/2a确定最佳售价75元。
光学设备调试 - 聚光镜焦距:凹面镜成像公式1/u+1/v=1/f可转化为v的二次方程,已知物距u和焦距f时计算像距v。
农业生产规划 - 灌溉区域最大化:用80米围栏靠墙建矩形菜地,设垂直墙边为x,面积S=x(80-2x),求导或配方法得x=20米时最大面积800㎡。
教学建议:讲解时可引导学生收集真实数据(如测量篮球投掷高度),用GeoGebra等工具可视化轨迹,通过改变系数观察曲线变化,深化对参数意义的理解。
