计算两个数的最大公约数是一个重要的数学问题,常用的方法是辗转相除法(欧几里得算法)。该方法的核心思想是:a和b是两个正整数,且a > b,则它们的最大公约数等于b和a对b的余数的最大公约数。通过不断将较大的数替换为较小的数与其余数的关系,最终会得到一个数,这个数即为最大公约数。这一方法不仅高效,而且容易实现,适用于任何两个正整数的情况。
一、最大公约数的定义与意义
最大公约数是指能够整除两个或多个整数的最大正整数。在数学和实际应用中,最大公约数常用于简化分数、解决整数问题以及计算最小公倍数等。了解最大公约数的概念,有助于提升解决问题的能力,特别是在数论和代数中。
二、计算最大公约数的方法
计算两个数的最大公约数可以使用几种主要方法:辗转相除法、质因数分解法和更相减损法。辗转相除法是最常用的方法,时间复杂度低,适合大数运算。质因数分解法则是将两个数分解为质因数后,找到共同的因数并取其乘积,适合小数的计算。更相减损法则是通过持续减去较小的数来简化计算,适用于特定情况。
三、最大公约数的应用
最大公约数在许多实际问题中都有重要应用,特别是在简化分数和解决比例问题时。它在计算机科学中的算法设计、信号处理、数据压缩等领域也扮演着关键角色。掌握最大公约数的计算方法,不仅对学习数学有帮助,也对其他学科的研究和应用具有指导意义。
相关问答FAQs
问:如何使用辗转相除法计算两个数的最大公约数?
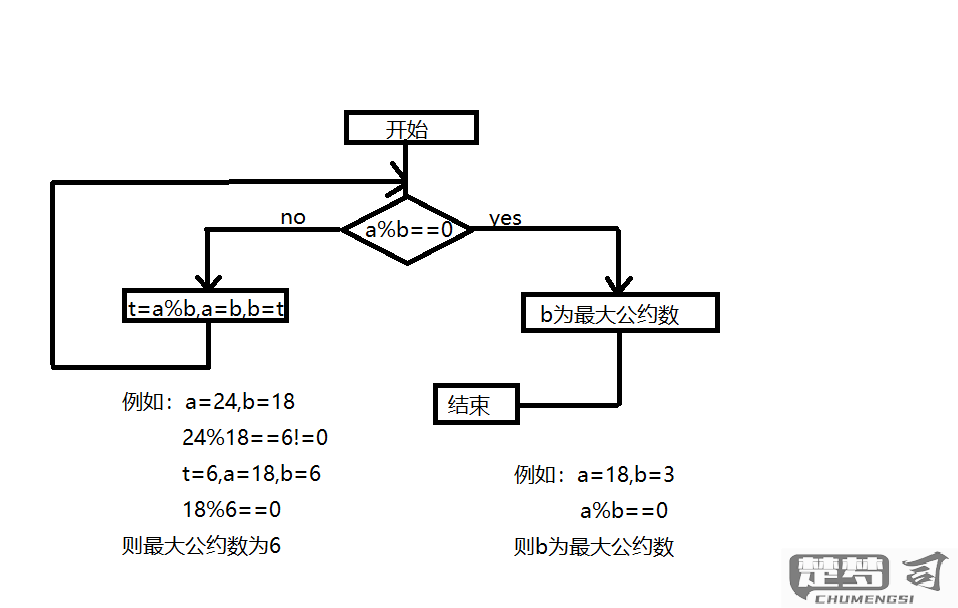
答:将两个数a和b进行比较,确保a > b。计算a除以b的余数r,将a替换为b,b替换为r。重复这个过程,直到b为0,a即为最大公约数。
问:最大公约数和最小公倍数有什么关系?
答:最大公约数和最小公倍数之间存在以下关系:对于任意两个正整数a和b,有公式:最大公约数(a, b) × 最小公倍数(a, b) = a × b。这表明它们在数值上是互为补充的。
问:最大公约数可以用于哪些实际应用?
答:最大公约数广泛应用于分数简化、比例问题、算法设计等领域,能够帮助解决多个数的整除问题,在计算机科学、工程和日常生活中都有重要意义。
