一、欧几里得算法的原理
欧几里得算法是一种古老而有效的算法,其核心思想是利用取余运算来逐步缩小问题的规模。假设我们有两个数a和b,b为0,那么gcd(a, b)就是a本身;b不为0,则可以将问题转化为gcd(b, a % b)。通过不断进行取余运算,最终会找到最大公约数。这种算法的时间复杂度为O(log(min(a, b))),在处理大数时仍能保持高效。
二、C语言实现示例
在C语言中实现最大公约数的代码非常简单,可以通过递归或者循环的方式来完成。以下是一个使用递归的示例:
```c
#include
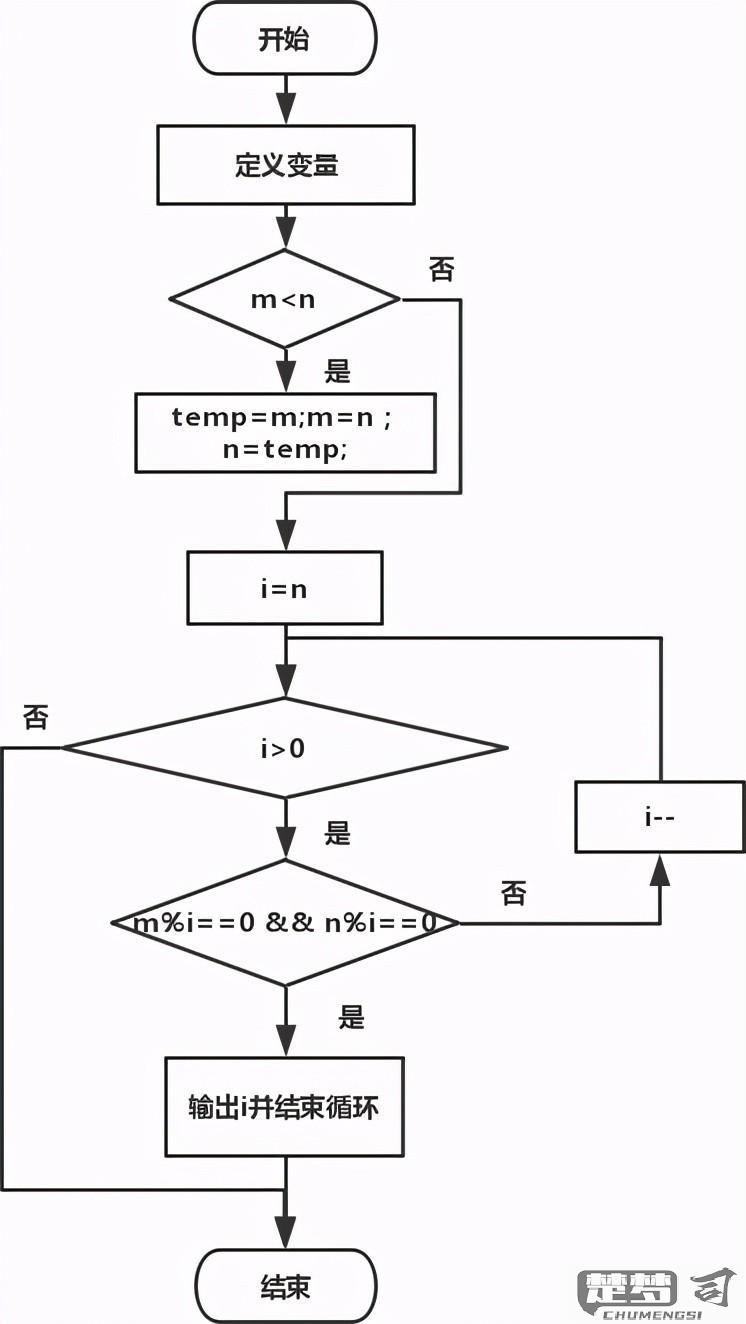
该代码定义了一个gcd函数,它接受两个整数作为参数,返回它们的最大公约数。在main函数中,调用gcd并输出结果。
三、应用场景及重要性
最大公约数在数论中具有重要地位,广泛应用于分数化简、求解最小公倍数等问题。在计算机科学中,最大公约数的算法也常被用作数据加密、哈希函数等领域。了解最大公约数的计算方法,不仅有助于提高编程能力,也能深入理解算法分析和复杂性。
相关问答FAQs
Q1: 最大公约数的计算是否有其他方法?
A1: 除了欧几里得算法,还有其他方法,如质因数分解法,但这些方法在效率上不如欧几里得算法。质因数分解法需要先进行因数分解,时间复杂度较高,不适合大数计算。
Q2: 为什么要计算最大公约数?
A2: 最大公约数在数学中有着广泛的应用,特别是在简化分数、解决整数问题等方面。它在算法设计与分析中也扮演着重要角色。
Q3: 如何验证计算结果的正确性?
A3: 可以通过已知的数对进行手动计算,或者使用不同的方法计算同一对数的最大公约数,比较结果是否一致。编写单元测试也是验证程序正确性的一种有效方式。
