一个数的平方怎么算？详细步骤与实例解析

一个数的平方怎么算

计算一个数的平方是数学中最基础的操作之一，具体方法如下：

1. 基本概念
   平方指将一个数乘以它本身，数学表达式为：
   n² = n × n
   例如：5的平方是 5 × 5 = 25。

2. 整数平方计算
   - 直接相乘：如 8² = 8 × 8 = 64。
   - 连续奇数求和法（适用于自然数）：
   1² = 1
   2² = 1 + 3 = 4
   3² = 1 + 3 + 5 = 9
   规律为n²等于前n个连续奇数的和。

3. 小数平方计算
   先忽略小数点，按整数计算后补回小数位：
   - 例：0.7² = 0.7 × 0.7 = 0.49
   - 例：1.2² = 1.2 × 1.2 = 1.44（计算12²=144后移动两位小数）。

4. 负数平方计算
   负数的平方结果为正数：
   (-n)² = (-n) × (-n) = n²
   例：(-4)² = 16。

5. 快速计算技巧
   - 接近整十数的平方：
   如 98² = (100-2)² = 10000 - 400 + 4 = 9604（展开二项式）。
   - 个位为5的数的平方：
   末两位恒为25，前几位为n×(n+1)。如 65² = 6×7=42，结果为4225。

6. 编程实现（Python示例）
   `python def square(num):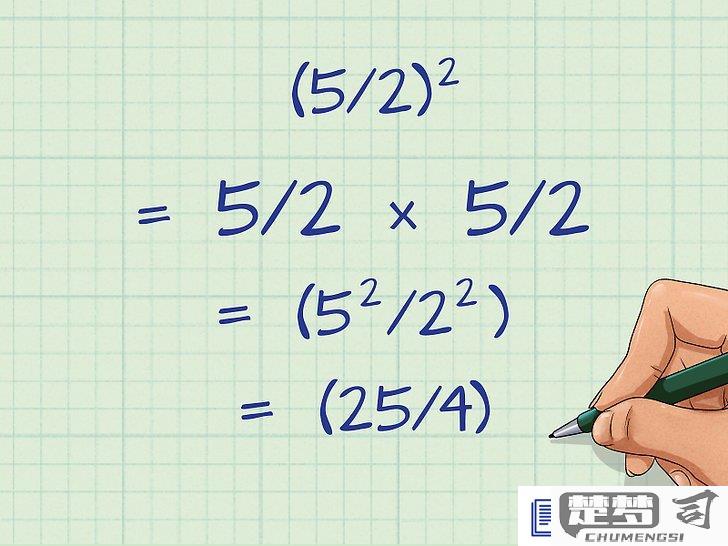

   

   return num ** 2  # 或 num * num
   

   print(square(9)) # 输出81 `

注意事项
- 大数平方可能超出计算器/编程语言的数据范围，需注意溢出问题。
- 无理数（如√2）的平方需保留精确形式或指定小数位数。

一个数的平方怎么算公式？

计算一个数的平方使用公式：
平方结果 = 原数 × 原数

步骤说明：
1. 确定需要计算平方的数字（记作x）
2. 将数字与自身相乘：x × x
3. 得到的结果即为该数的平方

示例：
- 计算5的平方：5 × 5 = 25
- 计算-3的平方：-3 × -3 = 9（负负得正）

注意事项：
- 平方运算适用于所有实数（正数、负数、小数）
- 平方结果永远为非负数（因实数相乘时符号会抵消）
- 对小数平方时，结果位数可能增加（如0.5² = 0.25）

扩展应用：
- 快速计算：a² = (a + b)(a - b) + b²（当b为与a接近的数时简化运算）
- 编程实现：多数语言用x ** 2或pow(x, 2)函数

一个数的平方怎么算步骤？

计算一个数的平方可以按照以下步骤操作：

1. 确定需要计算平方的数字，记作n
2. 将数字n与自身相乘，即n×n
3. 得到的结果就是该数的平方

示例计算过程： - 计算5的平方： 5 × 5 = 25 - 计算-3的平方： -3 × -3 = 9（负数相乘结果为正数） - 计算0.5的平方： 0.5 × 0.5 = 0.25

注意事项： - 平方运算适用于所有实数 - 负数的平方结果为正数 - 小数的平方结果会比原数更小 - 平方运算优先级高于加减法

特殊情形处理： - 计算带分数平方时，建议先转换为假分数 - 计算代数表达式平方时，注意使用完全平方公式

一个数的平方怎么算例子？

计算一个数的平方需要将该数乘以自身。具体步骤如下：

1. 确定要计算的数字（假设为n）
2. 进行乘法运算：n × n
3. 得到的结果就是该数的平方

实际计算示例： - 5的平方：5 × 5 = 25 - 12的平方：12 × 12 = 144 - 0.5的平方：0.5 × 0.5 = 0.25 - (-3)的平方：(-3) × (-3) = 9

注意事项： - 负数的平方结果为正数 - 小数的平方结果会比原数更小 - 计算时可以列竖式确保准确性 - 对于较大数字，可以使用计算器验证结果