
特征值为0可以推出什么
特征值为0可以推出矩阵是奇异的。在矩阵理论中,一个矩阵的特征值为0,意味着该矩阵不满秩,也就是说矩阵的行或列向量线性相关。这一特性直接导致矩阵的逆不存在,从而使得其在许多线性代数应用中表现出特定的行为...

特征值为0的特征向量有几个
特征值为0的特征向量个数通常与矩阵的秩有关。来说,一个矩阵的秩为r,那么它的特征值为0的特征向量的个数为n-r,其中n是矩阵的维度。这意味着,特征值为0的特征向量实际上对应着矩阵的零空间(nulls...
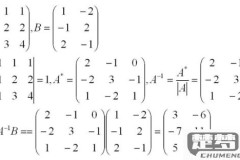
已知特征值求行列式的值
已知特征值求行列式的值是线性代数中的一个重要概念。对于一个n阶方阵A,其行列式的值可以通过其特征值来计算。若A的特征值为λ1,λ2,…,λn,则A的行列式等于所有特征值的乘积,即:det(A)...

知道三个特征值如何求A
知道三个特征值如何求矩阵A,首先需要利用特征值的性质。假设特征值为λ1、λ2、λ3,矩阵A的特征多项式可以表示为P(λ)=(λ-λ1)(λ-λ2)(λ-λ3)。通过对特征多项式展开,可...

已知三个特征值和一个特征向量
已知三个特征值和一个特征向量,这在数学和工程领域中具有重要的意义。特征值和特征向量是线性代数的核心概念,它们在许多应用中起到关键作用,例如在主成分分析、图像处理和系统稳定性分析中。特征值反映了线性变换...

已知特征值和特征向量怎么求矩阵
已知特征值和特征向量可以通过特征值分解来求出矩阵。步骤如下:1.设特征值为λ,特征向量为v,构建方程(A-λI)v=0。2.通过求解上述方程可以得到矩阵A的特征空间。3.通过组合已知的特...
