三角形的体积怎么算？理解三角形在三维空间中的体积计算

三角形的体积怎么算

三角形是二维图形，没有体积概念。体积是三维物体占据的空间大小，计算体积需要三维几何体如立方体、球体、棱锥等。

若需计算与三角形相关的三维物体体积，常见情况如下：

1. 三棱柱（三角柱）体积公式： 体积 = 三角形底面积 × 柱体高度 其中三角形底面积可用海伦公式计算： 面积 = √[s(s-a)(s-b)(s-c)]，s=(a+b+c)/2

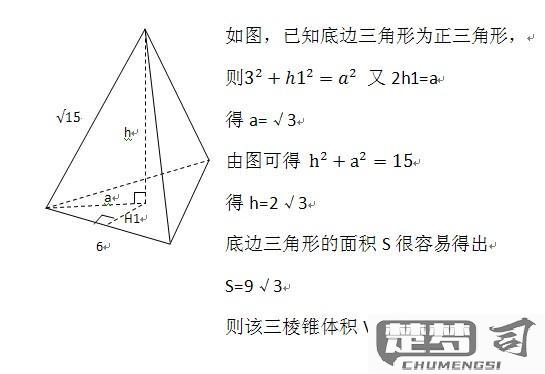
2. 三棱锥（四面体）体积公式： 体积 = (1/3) × 三角形底面积 × 锥体高度

3. 三角台（截头三棱锥）体积公式： 体积 = (1/3) × h × (A1 + A2 + √(A1×A2)) A1,A2分别为上下底面积

实际计算步骤： 1. 确认三维物体的具体类型 2. 测量必要的尺寸参数（边长/高度等） 3. 计算三角形底面积 4. 代入对应体积公式 5. 注意保持所有长度单位一致

若需计算特定三维物体的体积，请提供该物体的具体形状和尺寸参数。

三角形的体积计算公式是什么？

三角形是二维图形，没有体积概念。体积是三维空间的属性，适用于立体图形如棱锥、棱柱等。若需要计算与三角形相关的立体体积，可参考以下两种常见情况：

1. 三棱柱体积公式
   体积 = 三角形底面积 × 柱体高度
   示例：若底面为直角三角形，两直角边分别为3cm和4cm，柱高10cm，则
   体积 = (3×4÷2) × 10 = 60cm³

2. 三棱锥体积公式
   体积 = (三角形底面积 × 锥体高度) ÷ 3
   示例：若底面为等边三角形，边长5cm，锥高6cm，则
   体积 = (√3/4×5² ×6)÷3 ≈ 21.65cm³

注意事项：
- 计算前需确认三角形类型（普通/直角/等边）以正确求底面积
- 高度需垂直于底面测量
- 单位需统一（如全部转换为厘米）

若实际需求为其他立体图形（如三角台），需提供具体形状参数重新计算。

如何计算三维空间中三角形的体积？

计算三维空间中三角形的体积需要明确三角形在空间中的位置。由于三角形本身是二维图形，单独讨论其体积没有意义。实际上需要计算的是由三角形和空间某点（通常是坐标原点）构成的四面体的体积。

四面体体积计算公式： 给定三角形的三个顶点坐标A(x₁,y₁,z₁)、B(x₂,y₂,z₂)、C(x₃,y₃,z₃)，与原点O(0,0,0)构成的四面体体积V计算公式为：

V = (1/6) | (A × B) · C | 或展开为行列式形式： V = (1/6) | det(A,B,C) | 即： | x₁ y₁ z₁ | | x₂ y₂ z₂ | 的行列式绝对值乘以1/6 | x₃ y₃ z₃ |

计算步骤： 1. 构建3×3矩阵，每行为一个顶点坐标 2. 计算矩阵行列式： det = x₁(y₂z₃ - y₃z₂) - y₁(x₂z₃ - x₃z₂) + z₁(x₂y₃ - x₃y₂) 3. 取行列式绝对值 4. 乘以1/6得到体积

示例： 给定三角形顶点： A(1,0,0) B(0,1,0) C(0,0,1)

计算过程： | 1 0 0 | | 0 1 0 | = 1(1·1 - 0·0) - 0(0·1 - 0·0) + 0(0·0 - 1·0) = 1 | 0 0 1 |

体积V = (1/6)×|1| = 1/6

注意事项： - 顶点顺序影响行列式正负，但绝对值保证体积非负 - 若三点共线，行列式为0，此时不构成有效四面体 - 计算结果为与原点构成的四面体体积，不是三角形本身"体积"

三角形体积与面积的区别和联系？

三角形作为二维几何图形，其面积与体积的本质差异及关联可从以下维度进行解析：

核心概念差异 1. 数学维度 - 面积：二维空间的度量，单位为平方单位（㎡/cm²） - 体积：三维空间的度量，单位为立方单位（m³/cm³） 注：三角形本身不具备体积属性

1. 计算公式
   • 面积公式： S = (底边×高)/2 S = √[p(p-a)(p-b)(p-c)] （海伦公式）
   • 体积计算需转化为三维形态： 棱柱体积 = 底面积×高 棱锥体积 = 底面积×高/3

实际应用关联 1. 三维构建基础 - 当三角形作为多面体的底面时： - 柱体体积 = 三角形面积 × 柱体高度 - 锥体体积 = 三角形面积 × 锥体高度 / 3

1. 工程计算案例
   • 钢结构三角支撑件：
     • 表面积计算需分解为多个三角形
     • 用料体积 = 表面积 × 钢板厚度

常见误区澄清 1. 维度混淆 - 错误认知：直接计算"三角形体积" - 正确处理：必须明确三维形态（棱柱/棱锥等）

1. 单位换算陷阱
   • 面积单位平方与体积单位立方不可直接转换
   • 实际计算需引入第三维度参数

实操建议 1. 二维问题处理 - 测量至少三个参数（底边+高，或三边长度） - 优先验证三角形合法性（两边和>第三边）

1. 三维问题转换
   • 明确几何体类型（柱体/锥体/台体）
   • 建立三维坐标系时标注三角形所在平面