两个向量相乘怎么算？点积和叉积的计算方法详解

两个向量相乘怎么算

向量相乘主要有两种运算方式：点积（内积）和叉积（外积），具体计算方法如下：

一、点积（Dot Product）适用于两个维度相同的向量，结果为标量计算公式：A·B = Σ(a_i × b_i) = |A||B|cosθ 计算步骤： 1. 将两个向量对应分量相乘 2. 将所有乘积结果相加示例：向量A = [1, 2, 3] 向量B = [4, 5, 6] 点积 = 1×4 + 2×5 + 3×6 = 4 + 10 + 18 = 32

二、叉积（Cross Product）仅适用于三维向量，结果为向量计算公式： A×B = [a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1] 记忆方法：使用行列式计算： | i j k | | a1 a2 a3 | | b1 b2 b3 | 示例：向量A = [1, 2, 3] 向量B = [4, 5, 6] 叉积 = [(2×6)-(3×5), (3×4)-(1×6), (1×5)-(2×4)] = [12-15, 12-6, 5-8] = [-3, 6, -3]

注意事项： 1. 点积满足交换律，叉积不满足（A×B = -B×A） 2. 二维向量可视为z分量为0的三维向量计算叉积 3. 点积结果为0表示向量正交，叉积结果为0向量表示平行

两个向量相乘的数学公式是什么？

两个向量相乘主要有三种常见运算方式：

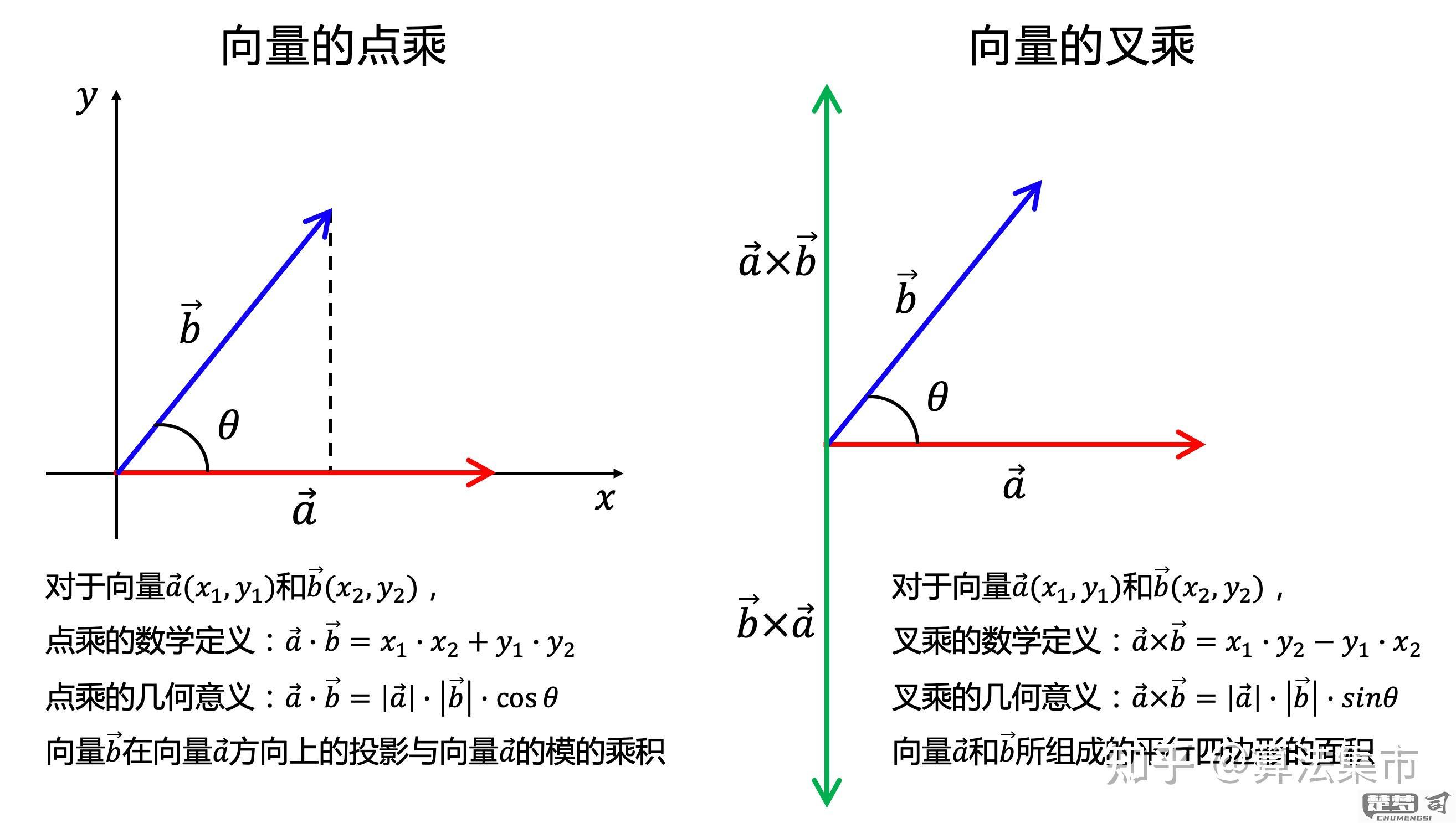
点积（内积） 公式：$\vec{a} \cdot \vec{b} = \sum_{i=1}^{n} a_i b_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n$ 性质： - 结果为标量 - 满足交换律：$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$ - 几何意义：$\vec{a} \cdot \vec{b} = \|\vec{a}\| \|\vec{b}\| \cos\theta$
叉积（仅限三维向量） 公式： $$\vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \ a_x & a_y & a_z \ b_x & b_y & b_z \end{vmatrix} = (a_yb_z - a_zb_y)\hat{i} - (a_xb_z - a_zb_x)\hat{j} + (a_xb_y - a_yb_x)\hat{k}$$ 性质： - 结果为向量 - 方向垂直于原向量平面（右手定则） - 大小等于$\|\vec{a}\| \|\vec{b}\| \sin\theta$
哈达玛积（逐元素积） 公式：$(\vec{a} \circ \vec{b})_i = a_i b_i$ 性质： - 结果为同维向量 - 常用于矩阵运算 - 不改变向量维度

计算示例（二维向量）： $\vec{a} = [2, 3], \vec{b} = [4, 5]$ - 点积：$2×4 + 3×5 = 23$ - 哈达玛积：$[8, 15]$

向量点乘和叉乘的区别是什么？

向量点乘（内积）和叉乘（外积）是两种完全不同的向量运算，主要区别体现在以下方面：

运算结果类型 - 点乘结果为标量（一个数值） - 叉乘结果仍为向量（三维空间中）
数学定义 - 点乘：a·b = |a||b|cosθ - 叉乘：a×b = |a||b|sinθ·n（n为垂直于a,b平面的单位向量）
几何意义 - 点乘反映两个向量的相似程度： 正值为同向 负值为反向 0表示垂直 - 叉乘得到的是与两个原始向量都垂直的新向量： 方向由右手定则确定 * 大小等于两向量张成的平行四边形面积
运算性质 - 点乘满足交换律：a·b = b·a - 叉乘不满足交换律：a×b = -b×a
典型应用场景 - 点乘常用于： 计算投影长度 判断向量夹角 光照模型中的漫反射计算 - 叉乘常用于： 计算法向量 判断向量相对方位 计算力矩/旋转
维度限制 - 点乘适用于任意维度空间 - 叉乘仅在三维空间有明确定义（七维空间有类似推广）
坐标计算公式（三维空间） `python

dot = a.xb.x + a.yb.y + a.z*b.z

cross = Vector(

   a.y*b.z - a.z*b.y,
   a.z*b.x - a.x*b.z,
   a.x*b.y - a.y*b.x

) `

实际应用时需特别注意：点乘可以用于计算夹角但会丢失方向信息，叉乘可以判断左右关系但会丢失长度信息。

如何计算两个向量的点乘和叉乘？

向量的点乘（内积）和叉乘（外积）是线性代数中的基础运算，计算方法如下：

点乘计算（适用于同维度向量） 1. 代数定义：对于向量a=[a₁,a₂,a₃]和b=[b₁,b₂,b₃]，点乘结果为a·b = a₁b₁ + a₂b₂ + a₃b₃ 2. 几何意义：a·b = |a||b|cosθ，θ为两向量夹角 3. 计算步骤： - 对应分量相乘 - 将所有乘积结果相加 4. 示例：向量a=[1,2,3]，b=[4,5,6] a·b = 1×4 + 2×5 + 3×6 = 4+10+18 = 32

叉乘计算（仅适用于三维向量） 1. 代数定义： a×b = [a₂b₃-a₃b₂, a₃b₁-a₁b₃, a₁b₂-a₂b₁] 2. 几何意义： - 结果向量垂直于a和b所在平面 - 模长|a×b|=|a||b|sinθ 3. 记忆方法：使用行列式计算： |i j k| |a₁ a₂ a₃| |b₁ b₂ b₃| 4. 示例：向量a=[1,2,3]，b=[4,5,6] a×b = [(2×6-3×5), (3×4-1×6), (1×5-2×4)]