标准正态分布表怎么查
标准正态分布表(Z表)的查询方法可分为以下步骤:
理解Z值含义 - Z值代表数据点与均值的标准差距离 - 正Z值表示高于均值 - 负Z值表示低于均值
表格结构识别 - 首列显示Z值的整数和小数点后第一位 - 首行显示Z值小数点后第二位 - 行列交叉处的数值表示P(Z≤z)的概率
具体查询步骤 - 将Z值拆分为两部分:例如Z=1.96拆分为1.9和0.06 - 在首列找到1.9所在行 - 在首行找到0.06所在列 - 行列交叉处的0.9750即为P(Z≤1.96)
负Z值处理 - 使用公式P(Z≤-z)=1-P(Z≤z) - 例如查Z=-1.96时: 先查1.96得0.9750 1-0.9750=0.0250
区间概率计算 - P(a≤Z≤b)=P(Z≤b)-P(Z≤a) - 例如P(0≤Z≤1.96)=0.9750-0.5=0.4750
实用技巧 - 多数Z表只显示正Z值部分 - 概率值通常保留4位小数 - 超出表格范围的极值可近似取0或1
电子表格替代方案 - Excel中使用=NORM.S.DIST(z,TRUE) - R语言使用pnorm(z) - Python使用scipy.stats.norm.cdf(z)
常见误区提醒: - 混淆单侧概率与双侧概率 - 忽略Z值的正负号 - 错误理解概率值含义(表格给出的是累积概率)
标准正态分布表的使用方法?
标准正态分布表是统计学中用于查找标准正态随机变量概率的工具,掌握其使用方法需要理解三个核心要点:
表格结构解析 - 最左侧列显示Z值整数部分及第一位小数 - 顶部行显示Z值第二位小数 - 表格交叉点对应的数值表示P(Z≤z)的概率值
具体查询步骤 (1) 将普通正态变量X转换为标准正态变量Z Z = (X - μ)/σ 其中μ为均值,σ为标准差
(2) 确定Z值后分解为三位数 例:Z=1.25分解为1.2(行)和0.05(列)
(3) 在表中定位对应行列的交点值 1.2行与0.05列交点值为0.8944
实际应用案例 已知某考试平均分μ=75,标准差σ=10,求P(X≤85): (1) 计算Z=(85-75)/10=1.0 (2) 查表得P(Z≤1.0)=0.8413 (3) 即84.13%考生成绩≤85分
注意事项 - 负Z值查表时使用对称性:P(Z≤-a)=1-P(Z≤a) - 精确到小数点后四位 - 不同版本表格可能行列相反,需先确认表头说明
如何快速查找标准正态分布表?
要快速查找标准正态分布表,可以按照以下步骤操作:
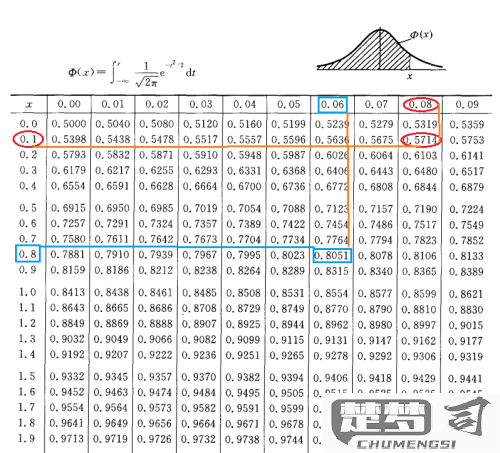
明确需求类型 - 已知Z值查概率:需要标准正态分布累积概率表 - 已知概率查Z值:需要标准正态分布分位数表
选择可靠来源 - 纸质版:统计学教材附录通常附有详细表格 - 电子版: 国家统计局官网统计用表栏目 高校数学系在线资源库 * 专业统计软件内置函数(如Excel的NORM.S.DIST)
具体查找方法(以Z=1.96为例):
横向表头定位整数位+第一位小数:1.9 纵向行首定位第二位小数:0.06 交叉单元格显示概率值:0.9750实用技巧 - 负值处理:利用Φ(-z)=1-Φ(z)性质转换 - 中间值估算:采用线性插值法 - 精度要求:四舍五入到小数点后四位
现代替代方案 - 计算器:TI-84等图形计算器内置功能 - 编程实现:
`python from scipy.stats import norm print(norm.cdf(1.96)) # 输出0.975002`
注意事项: - 确认表格是单侧还是双侧概率 - 注意表格标注的概率区域范围 - 新版表格可能使用1-α的表示方式
标准正态分布表查表技巧?
掌握标准正态分布表查表技巧需要理解三个核心要素:表的结构、数值对应关系以及反向查表方法。
标准正态分布表通常呈现的是Φ(z) = P(Z≤z)的累积概率值。表格左侧列显示z值的整数部分及第一位小数,顶部横栏显示z值的第二位小数。查找z=1.96时,先在左侧找到1.9行,再在顶部找到0.06列,交叉处对应的0.9750即为所求概率。
查表时需注意: 1. 表格可能只提供正数部分,利用对称性计算负数概率:Φ(-z)=1-Φ(z) 2. 对于z值超出表格范围(通常|z|>3.49)的情况,可直接取0或1 3. 需要计算区间概率时,使用P(a<Z<b)=Φ(b)-Φ(a)
反向查表(由概率求z值)步骤: 1. 在表格概率值中找到最接近给定概率的数值 2. 逆向查找对应的行和列标题 3. 对中间值可采用线性插值法提高精度
实际应用示例: 计算P(-1.5<Z<0.8)时: 1. 计算Φ(0.8)=0.7881 2. 计算Φ(-1.5)=1-Φ(1.5)=1-0.9332=0.0668 3. 最终结果=0.7881-0.0668=0.7213
建议练习时准备两种工具:传统印刷表格和电子计算器,前者帮助理解原理,后者提高实际工作效率。对于关键数据,建议通过不同来源交叉验证结果准确性。
标准正态分布表在线查询工具?
关于标准正态分布表在线查询工具,推荐以下几种实用资源:
Stat Trek标准正态分布计算器 - 网址:https://stattrek.com/online-calculator/normal - 功能特点:支持输入Z值计算累积概率,或输入概率反查Z值,可视化图表展示结果区域
Wolfram Alpha概率计算引擎 - 查询语法:直接输入"P(Z<1.96)"或"inverse normal 0.975" - 优势:提供精确到小数点后15位的结果,支持自然语言查询
GeoGebra正态分布工具 - 交互地址:https://www.geogebra.org/m/zsp6vkta - 特色功能:可拖动参数实时观察分布曲线变化,适合教学演示
R语言在线编译器 - 使用代码:
pnorm(1.96)计算P(Z≤1.96) - 进阶功能:通过qnorm(0.975)实现反查,适合需要批量计算的专业用户手机端解决方案 - 推荐应用:Probability Distributions (iOS/Android) - 移动端优势:内置离线查询表,支持滑动调节Z值精度到0.01
使用建议: - 常规查表推荐Stat Trek工具,界面最接近传统Z表形式 - 需要高精度计算时选择Wolfram Alpha - 教学演示场景优先使用GeoGebra的动态可视化 - 查询历史记录会自动保存在浏览器本地存储中
注意事项: - 部分工具需要允许浏览器运行JavaScript - 国际版工具注意切换小数点显示格式(点号/逗号) - 双边检验时需自行将显著性水平α除以2后查询
标准正态分布表查不到怎么办?
当标准正态分布表查不到所需数值时,可以考虑以下替代方案:
使用统计软件
- R语言:pnorm(z)函数可直接计算标准正态分布概率
- Python:scipy.stats.norm.cdf(z)提供相同功能
- Excel:NORM.S.DIST(z,TRUE)实现查表功能在线计算工具
- Stat Trek的Normal Distribution Calculator
- Wolfram Alpha输入"P(Z<z)"
- GeoGebra概率计算器近似计算法
当|z|>3时可采用以下近似公式:
P(Z>z) ≈ (1/z - 1/z³) * φ(z)
其中φ(z)为标准正态密度函数插值法处理中间值
对于介于表格数值之间的z值:
- 线性插值:P(z) ≈ P(z₁) + (z-z₁)(P(z₂)-P(z₁))/(z₂-z₁)
- 需确保|z₂-z₁|<0.01以保证精度反查临界值
若需要根据概率查z值:
- R使用qnorm(p)
- Python用scipy.stats.norm.ppf(p)
- Excel公式NORM.S.INV(p)
建议优先使用统计软件,其计算精度可达10^-16,远高于传统查表法的4位小数精度。对于考试等必须查表的情况,应选择最新版的分布表(通常附在教材附录),新版表格通常包含更多小数位和更广的数值范围。
标准正态分布表与概率计算关系?
标准正态分布表(Z表)与概率计算的关系体现在通过查表可直接获得标准正态随机变量Z落在特定区间的概率。标准正态分布均值为0,标准差为1,其概率密度函数呈钟形对称。
核心关系解析
1. Z值定义
Z值表示数据点距离均值的标准差倍数,计算公式为Z=(X-μ)/σ。通过Z值转换,任何正态分布均可标准化为标准正态分布。
查表逻辑
- 标准正态分布表通常提供P(Z≤z)的累积概率值。例如Z=1.96对应概率0.9750,表示Z≤1.96的概率为97.5%。 - 负Z值概率通过对称性计算:P(Z≤-a)=1-P(Z≤a)。典型概率计算场景
- 单侧概率:直接查表获取P(Z≤a)或P(Z≥a)=1-P(Z≤a)。
- 区间概率:P(a≤Z≤b)=P(Z≤b)-P(Z≤a)。
- 双侧概率:如P(|Z|≥a)=2×[1-P(Z≤a)]。
实操步骤示例
计算P(-1.5≤Z≤0.8):
1. 查表得P(Z≤0.8)=0.7881
2. 计算P(Z≤-1.5)=1-P(Z≤1.5)=1-0.9332=0.0668
3. 结果=0.7881-0.0668=0.7213
注意事项
- 不同Z表可能采用不同格式(如有的提供P(0≤Z≤a))。
- 精确计算建议使用统计软件,查表可能存在四舍五入误差。
- 对于非标准正态分布,需先进行Z转换再查表。
