空间直线的法向量有无穷多个。在三维空间中，直线的法向量并不是唯一的。给定一条直线，存在无穷多条法向量可以与之垂直。若已知直线的方向向量，则任何与该方向向量垂直的向量都可以作为法向量。这样的性质使得空间直线的法向量在几何学和物理学中具有广泛的应用。
一、空间直线的定义与法向量的概念
空间直线是由两个点确定的无限延伸的直线。在三维空间中，直线可以用参数方程或向量方程表示。法向量则是指与直线方向向量垂直的向量。直线的方向向量和法向量的关系是理解空间几何的重要基础。
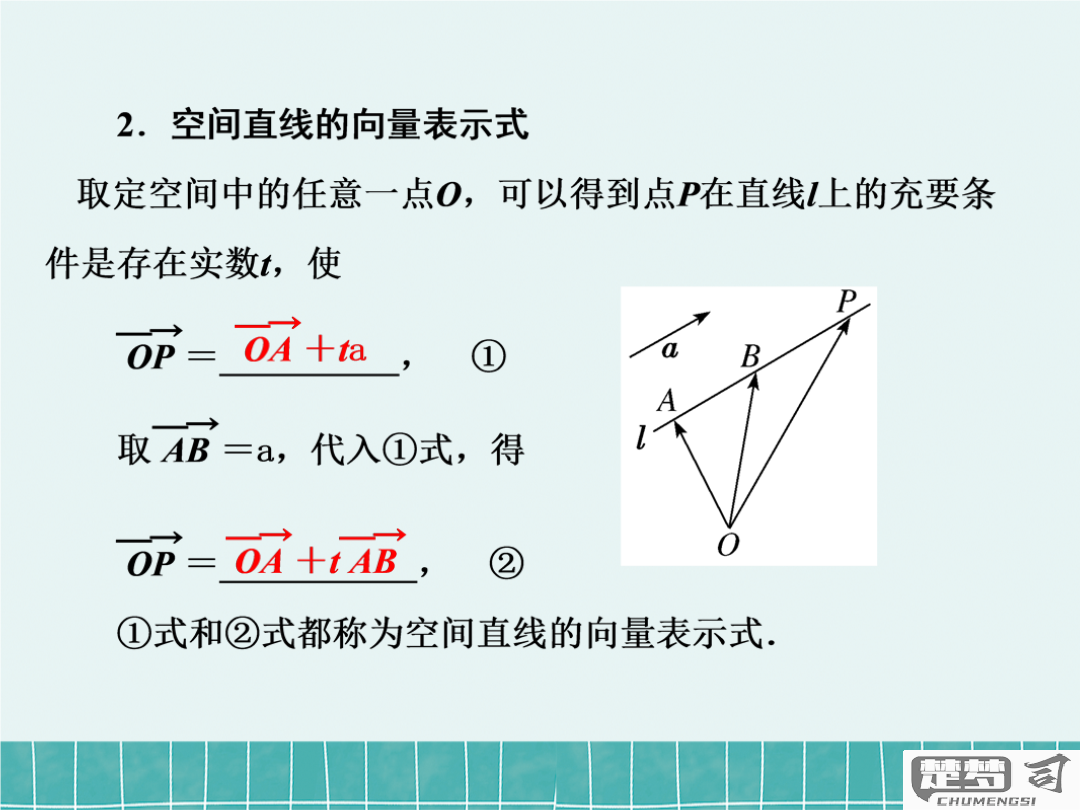
二、如何求得法向量
求得空间直线的法向量需要先明确直线的方向向量。设直线的方向向量为v，可以通过向量叉乘方法得到与之垂直的法向量。选择另一个不与v平行的向量u，则法向量可以通过计算v × u得到。这样可以得到多个法向量。
三、法向量在应用中的重要性
法向量在物理学中有着重要的应用，在计算面与直线的交点、确定力的方向等方面。更广泛地说，法向量在计算机图形学中也用于光照模型中，帮助模拟光线与表面的交互。理解空间直线的法向量及其性质，对于多个领域的研究和应用都具有重要意义。
相关问答FAQs
问：空间直线的法向量是否唯一？
答：空间直线的法向量不是唯一的，实际上存在无穷多个法向量，只要满足与直线的方向向量垂直的条件即可。
问：如何判断一个向量是否为某条直线的法向量？
答：可以通过计算两个向量的点积来判断。点积为零，则说明这两个向量垂直，一个向量可以视为法向量。
问：法向量在实际应用中有哪些例子？
答：法向量广泛应用于物理学中的力学分析、工程中的结构设计以及计算机图形学中的光照计算等领域。
猜你感兴趣：
outlook邮箱账号
上一篇
2025年01月06日
电脑word文档在哪里打开
下一篇
2025年01月06日